RQE HOME PAGE
＞RQC
＞ＲＱＣで解析してみよう
| HOME | RQE | RQC | RDE | ＲＱＣダウンロード |
|
RQE HOME PAGE
＞RQC
＞ＲＱＣで解析してみよう
|
||||
|
ＲＱＣで品質管理的アプローチを仕事に取り入れよう 品質管理というと製造現場でのデータの管理や検査と考えている方が多いと思います。 また、今の自分の仕事に品質管理は関係ないと思っている方もたくさんいると思います。
しかし、品質管理の目的は、買い手が満足してくれる品質の製品やサービスを、もっとも経済的な水準でお客様に提供することであり、そのためには、社内の各部門が、品質の保持、改善に関わる（品質管理的アプローチを行う）必要があります。
では、品質管理的アプローチをするには、具体的にどのようにしたらよいのでしょうか。
品質管理の着眼点は、問題点を的確に把握し、変化に対応するということにあります。従来よかった結果が悪くなってきたのなら、そこには何らかの変化があります。
な るべくはやく変わったところを見つけて、それを元に戻す修正作業が必要です。また、ばらつきの減少させたい場合も、いつから悪くなってきたのか、何が原因なのかによって技術的な改善の方法が変わってきます。そのために必要となってくるのがデータの分析が必要です。
分析といっても、難しい計算は必要ありません。
ここでいう”分析”は、難しい計算ではなくグラフを作成することが中心です。皆さんの身の回りにはたくさんのデータがあると思いますが、数字をながめていてもなかなか内容を理解するのは難しいものです。しかし、たとえばデータを折れ線グラフにして見れば、傾向も周期的なものも、変化の具合も一目瞭然です。
データの中に隠されている情報が、問題を解決できるヒントになるかもしれません。変化を見たいのであれば、まずは折れ線グラフ（変数別グラフに入っています）を作成してみましょう。折れ線グラフは、調べようとしている特性値を縦軸にとり、横軸を時間軸としてデータを打点し、その点を線で結んだものです。
例・・・ 《設備の温度データ》
- 温度変化に周期的な変化があるのはなぜだろう？
- いつからから上昇傾向なのかな？
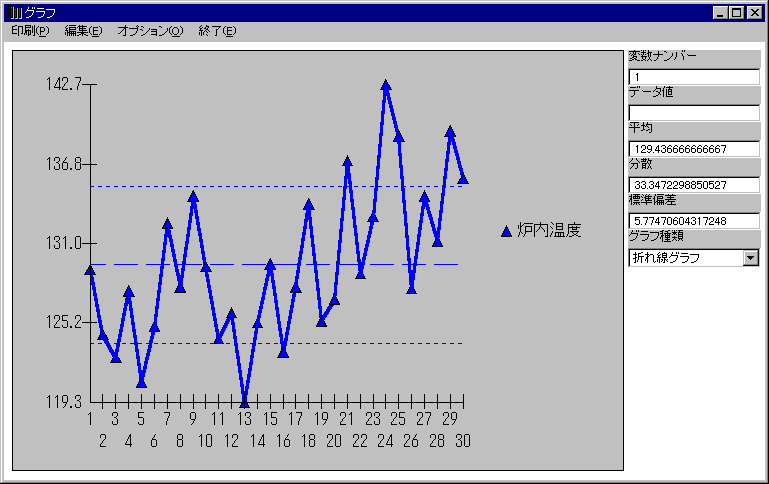
また、分類できるデータは、変数として分類し、結果を比較しましょう。ＲＱＣでは、平均値と標準偏差が点線で表示されますので、変数ごとのばらつきの比較もできます。
データの情報が数字で知りたいのであればグラフをクリックしてみましょう。クリックされたデータの値とそのグループの平均やばらつきの情報がグラフの右側に表示されます。
例・・・ 《対策前のデータと対策後のデータ》
- 対策後は、ばらつきが減少したな！
- 平均値はほとんどかわっていないな！
変数がおおいときは、変数別統計量グラフ（最大最小・標準偏差・平均による箱ひげ図）を作成してみれば、データ全体のばらつきのと平均値の比較をすることができます。
例・・・ 《製造メーカー別のデータ》
- Ａ社の部品のばらつきがおおきいみたいだ！
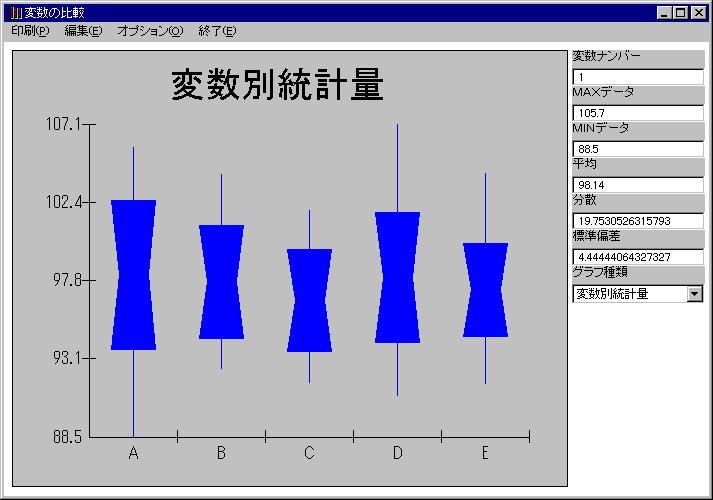
ここで紹介した折れ線グラフや変数別統計量グラフのほかにもＲＱＣでは、さまざまなグラフを手軽に作成することができます。
たとえば、データ全体の状況を把握するときは、ヒストグラムを使用します。
また、変数別ヒストグラムを利用すれば分布の比較をすることもできます。
例・・・ 《３台（Ａ，Ｂ，Ｃ）の機械で加工された部品データ》
- 変数別ヒストグラムでデータの分布の比較をしてみよう！
（変数別ヒストグラムとは、複数のヒストグラムをＺ軸上に配置し、分布の比較ができるよう工夫したグラフです。）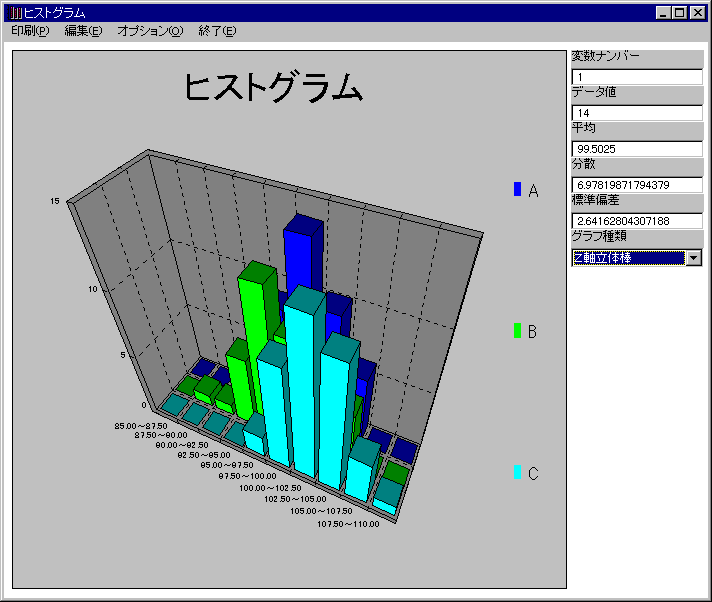
また、効率的に問題解決に取り組むには、影響の大きい項目から重点的に検討して改善することが大切です。どの項目の影響が大きいかを調べるためにはパレート図を使用します。
例・・・ 《原因別不良個数のデータ》
- 材料のクラックと硬度ムラに対策を打てば、ほぼ半数の不良をなくせるぞ！
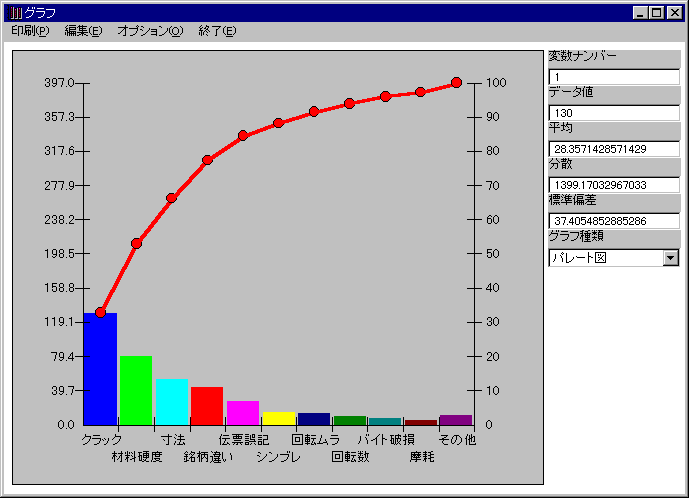
また、関連を分析したり、代用特性を見つけたいときは、散布図を利用するとよいでしょう。
（さらに詳しく解析をしたい場合は、相関分析・回帰分析なども実施することができます）
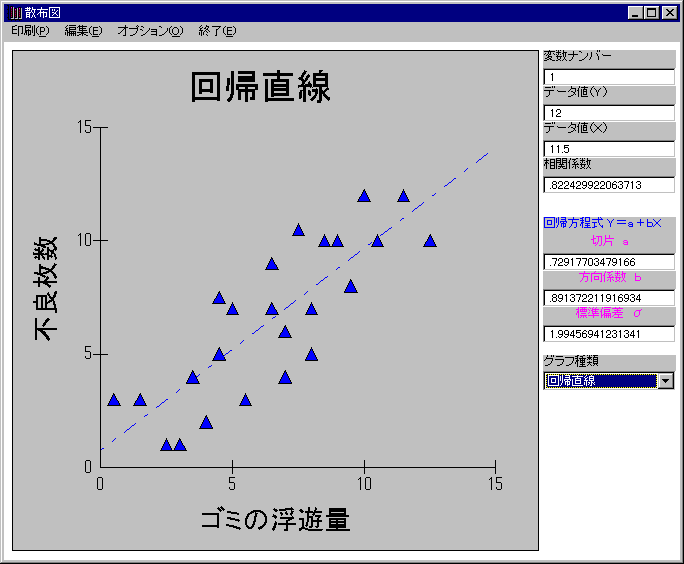
例・・・ 《ゴミの浮遊量と精密加工部品の不良枚数》
- 部品の不良枚数とゴミの浮遊量はやはり関係があるぞ！
ただ数字をならべているだけでは的確に状況を把握することは困難です。 その場に適応したグラフを作成することにより、いままで気づかなかった傾向や対策に気づくことがあります。
現状把握（効率的な作図）が、品質管理の第一歩です。さあ、ＲＱＣで品質管理的アプローチを仕事に取り入れてみましょう。
データ解析の手順 ＲＱＣでデータ解析を行う場合、まず解析に使用するデータを作成する必要があります。
データの新規作成を選択して、解析に使用するデータ情報（サンプル数と変数の数）を入力しましょう。入力された情報によってワークシートが作成されます。
分類できるデータは、変数として分類して入力します。サンプル数が、ワークシートの縦の数、変数の数がワークシートの横の数となります。
ワークシートが作成されたらデータ入力です。
データの入力が終わったら、解析に使用するグラフの種類をコンボボックスで選択し、グラフを作成します。
データの入力やデータの張り付け
解析に使用するデータ情報（サンプル数と変数の数）を入力しないと、データの入力やデータの貼り付けはできません。 まず、新規作成を選択して、ワークシートを作成してください。
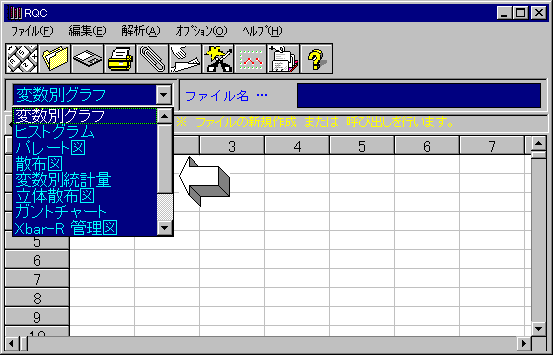
選択できるグラフには、
などがあります。 （それぞれのグラフの解析手順を表示するには、上記のグラフ名をクリックして下さい。）
- 変数別グラフ
- ヒストグラム
- パレート図
- 散布図（相関分析・回帰分析）
- 変数別統計量グラフ
- ガントチャート
- Ｘｂａｒ−Ｒ管理図
- Ｐ−Ｐｎ管理図
- 欠点数データ管理図
- Ｘ−Ｒｓ管理図
- 層別統計量グラフ
- 層別ヒストグラム
個々のグラフは、円グラフ・立体円グラフ・棒グラフ（縦横）・立体棒グラフ（縦横）・折れ線グラフ・エリアグラフ・帯グラフなど、さらに細かい指定を行うことができます。
いろいろな機能紹介 ＲＱＣには、品質管理で必要なグラフを作成する以外にも、さまざまな便利な機能があります。
いろいろな機能の一部をここでご紹介します。
- データ情報の表示
- データのマスク
- データラベルの設定
- グラフタイトルの設定
- グラフの最大・最小値の設定
- 行の挿入と削除
- グラフの印刷・コピー
- 凡例の表示
- ３Ｄグラフの視点設定
- 円グラフのセグメントの分離
- データの区分表示（斜線表示）
品質管理講座
第一回・・・現状を的確に把握しよう（１）
（変数別グラフ・変数別統計量グラフ）
（ヒストグラム）
（パレート図）
（散布図・相関分析・回帰分析）
（３σ線の活用・統計情報線）
（管理図）
（層別）
例題とその解析例
