
 |
データを分類しよう(層別) |
データをうまく活用するにはデータの履歴や背景を明らかにし分類を十分に行うことが大切です。
すなわち「この製品は、どの機械で誰がいつどのように加工したのか?」等、人別、機械別、原材料別、日付別など、技術的に影響を与えていると思われる原因別にグラフを描いてみることが、問題解決への手がかりとなります。
このようにいくつかのグループ(層)にデータを分類し解析を行うことを層別といいます。
RQCの多くのグラフでは、層別する必要があるデータや比較したいデータは、あらかじめそのクループ数を変数として指定し、変数ごとにデータの入力を行います。
しかし、データを入力した後層別が必要になったり、層別するグループのデータ数が異なるため最初に変数の数やサンプル数が指定できない場合はどうしたらよいでしょうか?
そのような場合、層別因子を利用し層別グラフを作成するとよいでしょう。
層別グラフでは、層別されていないデータに層別因子を対応してわりつけることにより、手軽にデータを層別しグラフを作成することができます。
今回は、この層別についてお話をしたいと思います。
●層別グラフ
以下のグラフは、ある部品の寸法データをヒストグラムにしたものです。
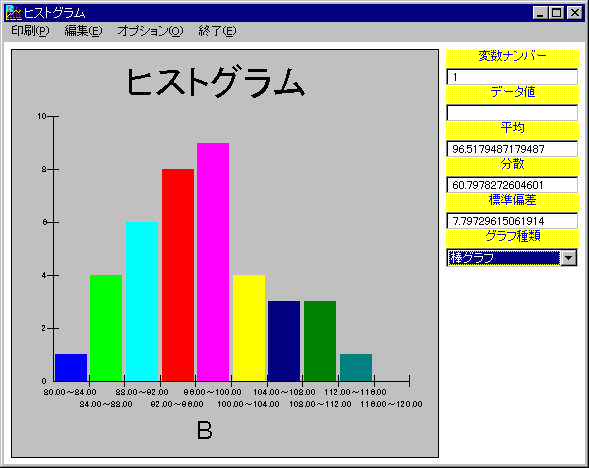
後日、このデータは3台の違う機械で加工された部品が混在していることが判りました。
技術的に影響を与えていると思われる要因がある場合は層別してみることによりその影響を把握することができます。
同じデータを層別グラフを利用し、解析してみましょう。
層別グラフでは、層別因子という考え方を使いデータを層別します。
層別因子とは1〜5の整数を使用し、対応するデータがどのグループに所属するのかを表したものです。
RQCはこの層別因子(1〜5の整数)によりデータを層別し、グラフを作成します。 以下のデータは変数Aを層別因子として変数Bのデータに対応させたものです。
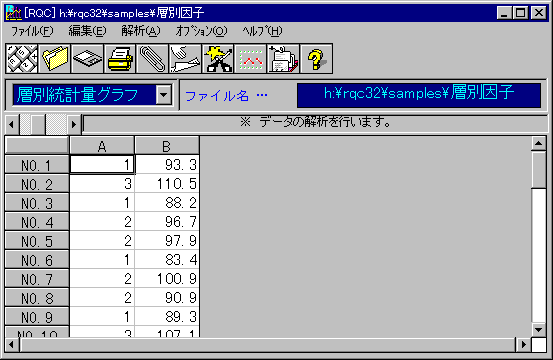
「NO.1のデータはグループ1に」「NO.2のデータはグループ3に」等、層別因子には層別するグループ番号を入力します。
RQCでは5グループまでの層別ができます。層別因子は1から5の整数を使用して下さい。
どの変数を層別因子として利用するかは、解析の段階で指定します。
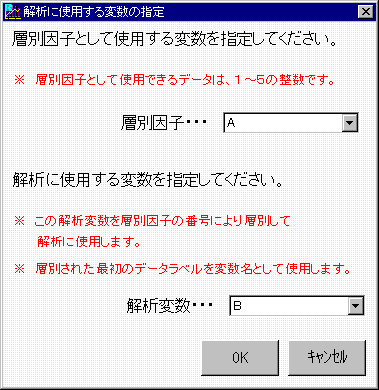
RQCでは、層別グラフとして、層別統計量グラフや層別ヒストグラムを用意していますので使用してみて下さい。
●層別統計量グラフ
層別統計量グラフは、層別されたグループごとの平均値・標準偏差・最大値・最小値をグラフ(箱ひげ図)にしたものです。
層別したデータの統計量の比較をすることができます。
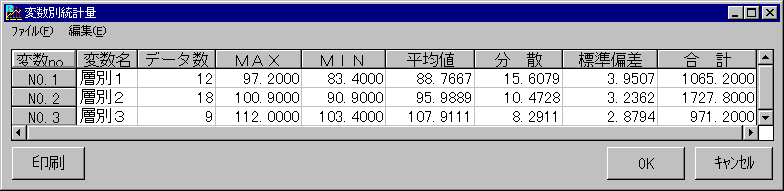
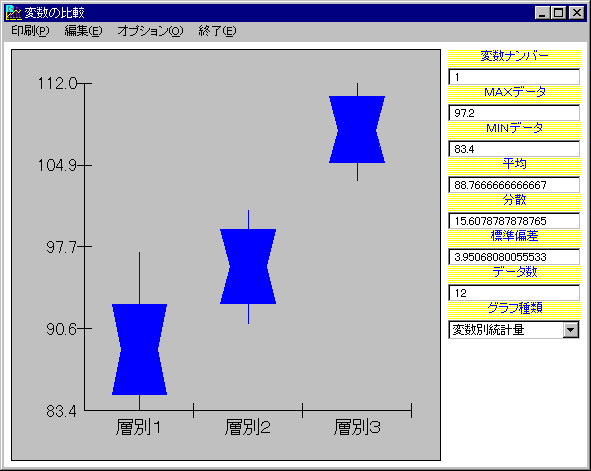
層別統計量グラフの構成は以下のようになっています。
●層別ヒストグラム
層別ヒストグラムは、層別されたグループごとのヒストグラムを作成し、平面やZ軸上で層別したデータの分布形状や分布位置の違いを比較することができます。
また積層型を選ぶことにより、層別する前のヒストグラムと層別後のデータの関係を把握することができます。
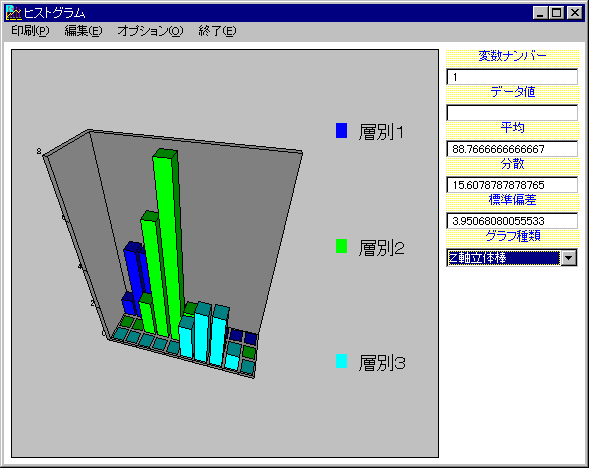
グラフ例・・・層別ヒストグラム(Z軸立体棒)
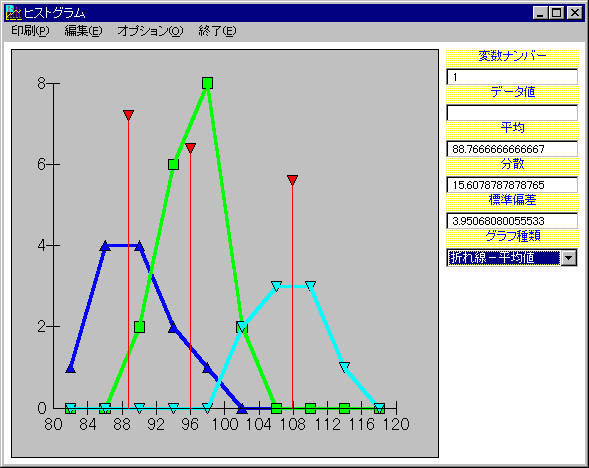
グラフ例・・・層別ヒストグラム(折れ線−平均値)
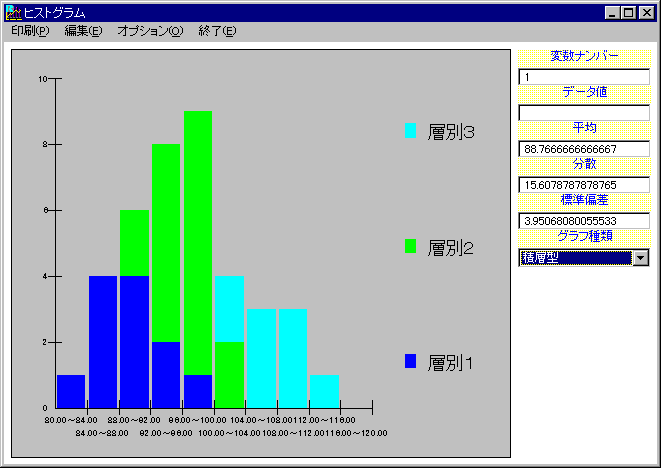
グラフ例・・・層別ヒストグラム(積層型)
的確な対応を行うには、このように技術的に影響を与えていると考えられる要因で層別することは非常に重要です。 中心値やばらつきの異なったサンプルが混在しているデータでは、管理も解析もできません。
層別をうまく行うことが品質管理の成功への手がかりとなると考えています。
品質管理講座 |
 |
 第一回・・・現状を的確に把握しよう(1) 第一回・・・現状を的確に把握しよう(1)(変数別グラフ・変数別統計量グラフ)
|
| ≪HOME≫ | ||||
| RDE | ||||