
 |
変数間の関係を調べよう |
2つの変数に対する平均値とばらつきの比較をする場合に、変数別グラフが有効だということを、「第一回・・・現状を的確に把握しよう(1)」でご説明しました。
では、比較ではなく、変数間の関係を調べるにはどうしたらよいでしょう。
たとえば、RQCのサンプルデータにも含まれている「ゴミの浮遊量と精密部品の不良枚数」などのように、組になって測定されたデータの場合です。
RQCでは、2つの変数間の関係や様子をつかむために散布図を用意しています。 散布図は、互いに関連する二つの変数の関係、すなわち対になった測定値(X,Y)をプロットしたものです。
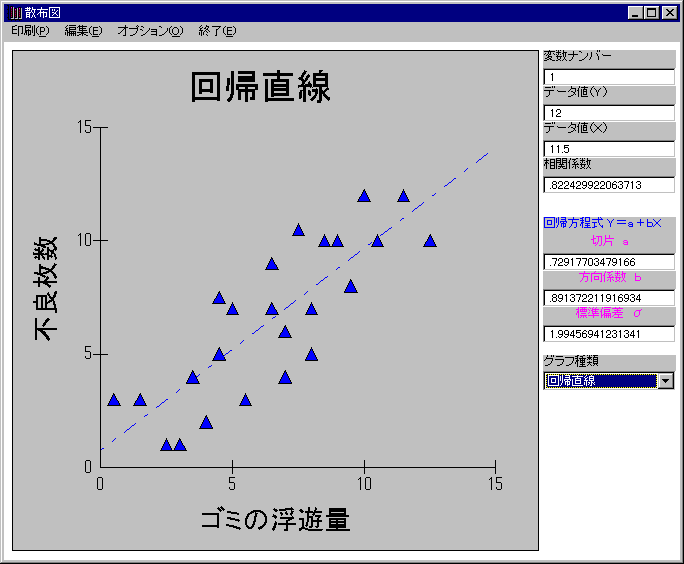
たとえば、以下の図は、ゴミの浮遊量が変化したときに精密部品の不良枚数がどう変化したかを対応をつけて散布図として出力したものです。
不良枚数を縦軸、ゴミの浮遊量を横軸として、データをプロットしています。
散布図を描いてみると、ゴミの浮遊量が増えると不良枚数が多くなるのが視覚的によくわかると思います。
●散布図を活用しよう
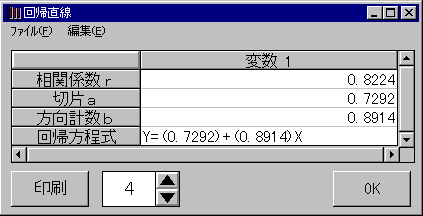
相関係数とは、特性Xと特性Yの関係の強さを数字として表したものです。
相関係数rの範囲は、マイナス1からプラス1で、数字が1のとき相関関係がもっとも強く、ゼロのとき無相関となります。
(相関係数がマイナスのときは負の相関となります。)
言い換えれば、プロットした点がすべて直線上にあれば、相関係数の絶対値は1、直線性がなくなるに応じて相関係数はゼロに近づきます。
相関関係が強く、特性値X(説明変数)を特性値Y(目的変数)の代用特性として利用したい場合や、2変数間の関係が、原因(説明変数)とその結果(目的変数)と考えられ、説明変数から目的変数を推定したいときのような場合は、回帰分析を行うことになります。
回帰分析とは、目的変数をY軸、説明変数をX軸にしてデータをプロットし、目的変数に説明変数の影響がどれくらいあるのかを分散分析という方法で定量的に求める方法です。
目的変数の変化に対する影響が大きければ、特性値Yを特性値Xによりコントロールしたり、特性値Yを特性値Xから推測することが可能になります。
上記の例ではゴミの浮遊量により、不良枚数を推定することが可能になるということです。
代用特性として利用する場合、必要となってくるのが回帰直線です。
回帰直線は、最小二乗法という考え方で、Y軸方向の誤差を最小にするよう作られた直線です。
つまり、特性Xを特性Yの代用特性として利用するときの中心となる直線です。RQCでは、グラフの種類を選択することにより、簡単に回帰直線を表示することができますので、利用してみてください。
回帰方程式・・・Y=a+bX
標準偏差σは、代用特性をどの範囲で管理するか決める場合に使用します。
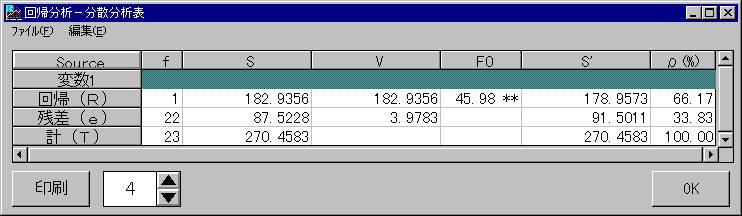
RQCでは、散布図を出力すると、下の表のような 分散分析表と回帰直線に関する情報が表示されます。
分散分析表は、全変動を回帰変動と残りの誤差変動に分解したものです。 回帰直線のあてはめの精度を詳しく知りたい場合に利用して下さい。
下記分散分析表より、ゴミの浮遊量が部品の不良枚数に及ぼす影響が約66パーセントに及んでいることがわかりました。
分散分析表の記号等については、
 の分散分析入門をご参照下さい。
の分散分析入門をご参照下さい。
|
|
|
相関関係は一つの事象を別の2つの面から見た代用特性の関係を示したものです。したがって、いくら散布図を作成したとき相関係数が大きいからといって、技術的根拠がない場合、本質的な相関があるとはいえません。このような疑似に注意してください。 また、散布図の打点が曲がっているような場合には相関関係を求めても意味はありません。 |
|
|
|
2つの変数間の分析には相関分析と回帰分析があります。
相関分析は、一つの事象を別の2つの面から見た代用特性の関係を示したもので、特性Xが増加すれば特性Yも増加するとかいった関係があるかないかを、統計的に調べることです。 これに対して、特性Xを原因、特性Yをその結果であると考えて、Xの関数としてYを求めることが、統計的に意味があるかどうかを調べることを回帰分析といいます。
実際の業務では、相関分析と回帰分析を平行して行う場合が多いようです。
|
品質管理講座 |
 |
 第一回・・・現状を的確に把握しよう(1) 第一回・・・現状を的確に把握しよう(1)(変数別グラフ・変数別統計量グラフ)
|
| ≪HOME≫ | ||||
| RDE | ||||