
 |
統計情報線を活用しよう |
ばらつきは、2つに分類することができます。 ひとつは、何かしらの原因、たとえば作業標準を守らなかったり、違う部品を使ってしまったり、技術的に原因を排除すれば、改善することができるばらつきです。
もうひとつは、いつもと同じように作業をしても結果がばらついてしまう偶然誤差によるばらつきです。
たとえば同じ仕様による原材料をもちいて、同一の作業標準のもとで製造された製品であっても、まったく同じ品質の製品はできません。それは、同じ仕様や作業であっても、必ず、避けられない範囲内でばらつきがあるからです。
このような避けられない条件の組み合わせでおこるばらつきを偶然によるばらつきと呼んでいます。
偶然のばらつきによる分布は、こちらのように計測データの大部分が中心付近にあり、中心から離れるに従いデータ数が少なくなり左右対称の形となっています。
●偶然によるばらつき
このようなばらつきの形を正規分布と呼んでいます。このような分布を標準偏差で図のように分けていくと、分布曲線に囲まれた全体の面積に対する割合が分かります。
言い換えると、偶然によるばらつきによる分布は、平均値と標準偏差でデータを区分したとき、その出現確立が、計算できるということです。
データが範囲内に出現する確立と範囲外に飛び出す確立は以下のようになります。
| 範 囲 | 範囲内に出現する確立 | 範囲外に飛び出す確立 |
| 平均値±1シグマ | 68.3% | 31.7% |
| 平均値±2シグマ | 95.4% | 4.6% |
| 平均値±3シグマ | 99.7% | 0.3% |
すなわち、正規分布に従うと考えられる場合、±1σ内にデータの68.3%が、±3σ内にデータの99.7パーセントが分布すると考えることができます。反対に、±3σより外に外れる確立は、0.3%(1000回に3回程度)であり、ほとんどのデータは、±3σに収まると考えてよいことになります。
このことから、±3σよりデータが飛び出すときは「分布が変わった」「母集団の平均値が変化した」と疑ってみる必要があります。
この考え方は、3シグマルールと呼ばれ、管理図の管理限界線算出の根拠となっています。
RQCでは、一変数グラフのグラフの変更で、3σ線が簡単に表示できるので表示してみてください。点線が±1シグマ、実線が±3σです。
●3シグマ線を表示してみよう
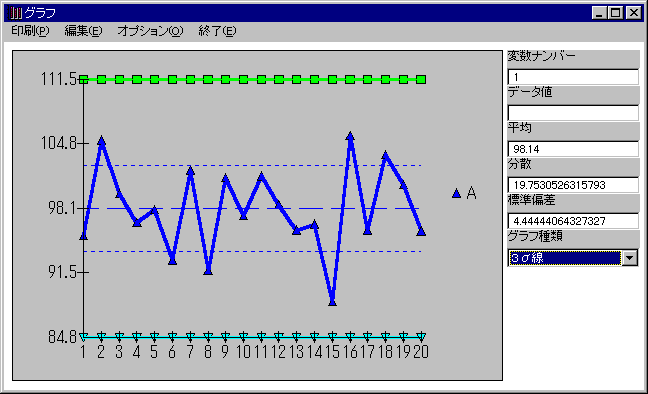
時系列で平均値が変化していると思われる場合は、統計情報線を活用するとよいでしょう。
折れ線グラフで、表示する統計情報を、【オプション】→【統計情報の設定】で選択してください。
統計情報の種類には、「平均値」「標準偏差」「最大最小値」「データの傾き(回帰直線)」があります。
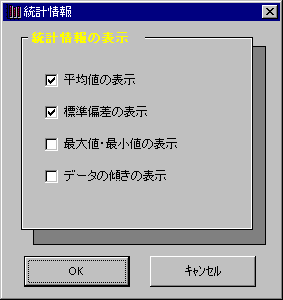
●統計情報線を活用しよう
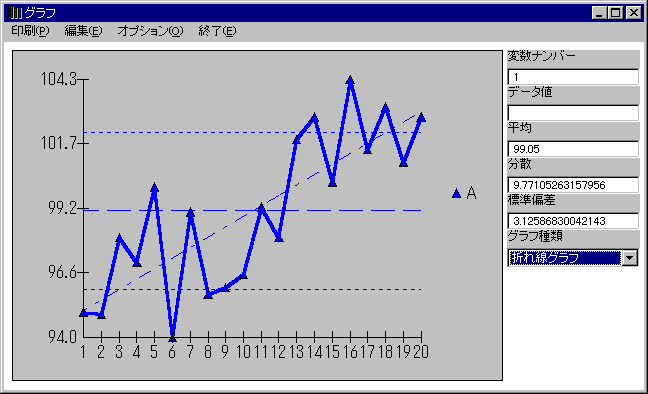
上の図は、「標準偏差」「平均値」「データ点の傾き」の統計情報線を表示をしたものです。
ばらつきの大きさと平均値の変化がよく分かると思います。「データ点の傾き」が大きい場合は何らかの原因で平均値が変化している可能性があります。
品質管理講座 |
 |
 第一回・・・現状を的確に把握しよう(1) 第一回・・・現状を的確に把握しよう(1)(変数別グラフ・変数別統計量グラフ)
|
| ≪HOME≫ | ||||
| RDE | ||||