
 |
最適条件を推定してみよう(2) |
前回は、平均値とばらつきを総合したSN比から最適条件を決める場合を、望小特性を例にご説明しました。
今回は、平均値とばらつきを別々に解析し、最適条件を求める手順を、望目特性の例題を使用してご説明したいと思いますと思います。
 |
例題2・・・望目特性 |
ビデオテープのバックテンション調整機構部の最適化をはかるため、次のような制御因子を取り上げ、理論式で計算を行なった。 このバックテンション調整機構では、テープの巻状態が変わってもテープテンションが変化せず、一定(24.5g)に保たれることが、理想である。
| 制 御 因 子 | 第1水準 | 第2水準 | 第3水準 |
| A.テープガイドとテープの摩擦係数 | 0.19 | 0.27 | − |
| B.BTバンドとリール台の摩擦係数 | 0.09 | 0.125 | 0.16 |
| C.テープガイドへのテープ巻付角(°) | 62 | 72 | 82 |
| D.リール台へのBTバンド巻付角(°) | 128 | 143 | 158 |
| E.リール台の制動部半径(mm) | 10.5 | 11.5 | 12.5 |
| F.BTレバーの長さ(mm) | 11.8 | 12.3 | 12.8 |
| G.BTバンド取付部のの長さ(mm) | 1.4 | 1.6 | 1.8 |
| H.バネによるBTレバーモーメント(g-mm) | 178 | 222 | 266 |
| 誤差因子 | リールへのテープの巻半径 | リール台の無負荷トルク |
| N1 | 21(mm) | 20(g-mm) |
| N2 | 13(mm) | 40(g-mm) |
《わりつけとデータ》
| A | B | C | D | E | F | G | H | N1 | N2 | |
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | |||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 15.74 | 21.78 |
| 2 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 18.57 | 24.44 |
| 3 | 1 | 1 | 3 | 3 | 3 | 3 | 3 | 3 | 21.28 | 26.94 |
| 4 | 1 | 2 | 1 | 1 | 2 | 2 | 3 | 3 | 24.22 | 31.63 |
| 5 | 1 | 2 | 2 | 2 | 3 | 3 | 1 | 1 | 17.97 | 21.47 |
| 6 | 1 | 2 | 3 | 3 | 1 | 1 | 2 | 2 | 20.56 | 25.36 |
| 7 | 1 | 3 | 1 | 2 | 1 | 3 | 2 | 3 | 27.60 | 33.53 |
| 8 | 1 | 3 | 2 | 3 | 2 | 1 | 3 | 1 | 18.65 | 22.68 |
| 9 | 1 | 3 | 3 | 1 | 3 | 2 | 1 | 2 | 22.54 | 26.08 |
| 10 | 2 | 1 | 1 | 3 | 3 | 2 | 2 | 1 | 16.67 | 21.22 |
| 11 | 2 | 1 | 2 | 1 | 1 | 3 | 3 | 2 | 15.15 | 20.67 | 12 | 2 | 1 | 3 | 2 | 2 | 1 | 1 | 3 | 21.85 | 26.73 |
| 13 | 2 | 2 | 1 | 2 | 3 | 1 | 3 | 2 | 21.85 | 27.21 |
| 14 | 2 | 2 | 2 | 3 | 1 | 2 | 1 | 3 | 25.26 | 29.49 |
| 15 | 2 | 2 | 3 | 1 | 2 | 3 | 2 | 1 | 14.45 | 17.58 |
| 16 | 2 | 3 | 1 | 3 | 2 | 3 | 1 | 2 | 24.80 | 27.99 |
| 17 | 2 | 3 | 2 | 1 | 3 | 1 | 2 | 3 | 26.55 | 30.82 |
| 18 | 2 | 3 | 3 | 2 | 1 | 2 | 3 | 1 | 15.36 | 18.39 |
SN比は最適設計のための測度であり、感度Sは必要なときに、出力の平均値を目標値に合せるための調整因子を選ぶために使用します。
この例題で、「RQE」の出力から最適条件を求めてみましょう。
「RQE」の出力(SN比)
分散分析表(分散2.5以下をプーリング)
| Source | f | S | V | F0 | S' | ρ(%) |
| A | 1 | 6.8091 | 6.8091 | 6.00 | 5.6742 | 6.17 |
| B | 2 | 52.3043 | 26.1522 | 23.04 | 50.0344 | 54.45 |
| D | 2 | 5.9501 | 2.9751 | 2.62 | 3.6803 | 4.01 |
| G | 2 | 15.4788 | 7.7394 | 6.82 | 13.2089 | 14.37 |
| e | 10 | 11.3493 | 1.1349 | - | 19.2938 | 21.00 |
| T | 17 | 91.8917 | 91.8917 | 100.00 |
工程平均
| 因子名 | 水準1 | 水準2 | 水準3 |
| A | 16.1771 | 17.4072 | |
| B | 14.6428 | 16.9214 | 18.8123 |
| C | 16.2107 | 16.8719 | 17.2939 |
| D | 16.1213 | 16.7297 | 17.5255 |
| E | 16.1225 | 16.8724 | 17.3816 |
| F | 16.5118 | 16.8031 | 17.0616 |
| G | 17.9860 | 16.6654 | 15.7251 |
| H | 16.3794 | 16.8556 | 17.1414 |
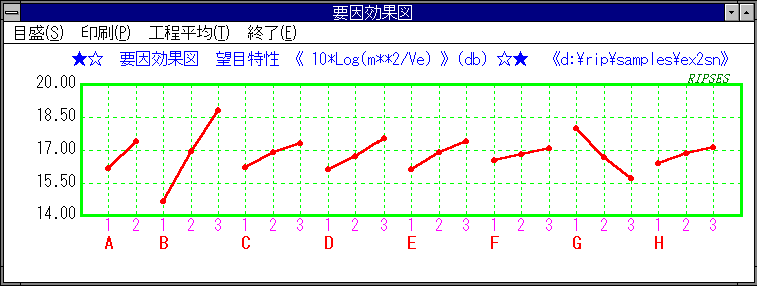
要因効果図
「RQE」の出力(感度)
分散分析表(分散1.5以下をプーリング)
| Source | f | S | V | F0 | S' | ρ(%) |
| B | 2 | 5.4760 | 2.7380 | 6.25 | 4.5995 | 9.60 |
| C | 2 | 3.9237 | 1.9618 | 4.48 | 3.0472 | 6.36 |
| H | 2 | 33.7126 | 16.8563 | 38.46 | 32.8361 | 68.50 |
| e | 11 | 4.8206 | 0.4382 | - | 7.4501 | 15.54 |
| T | 17 | 47.9329 | 47.9329 | 100.00 |
工程平均
| 因子名 | 水準1 | 水準2 | 水準3 |
| A | 27.2223 | 26.7415 | |
| B | 26.2687 | 27.0650 | 27.6121 |
| C | 27.5833 | 26.9173 | 26.4452 |
| D | 26.6702 | 27.0021 | 27.2735 |
| E | 26.7290 | 26.9672 | 27.2496 |
| F | 27.2201 | 26.9703 | 26.7553 |
| G | 27.2845 | 27.0115 | 26.6498 |
| H | 25.2538 | 27.0912 | 28.6007 |
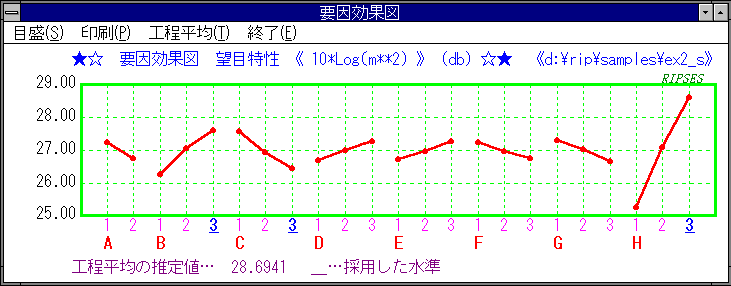
要因効果図
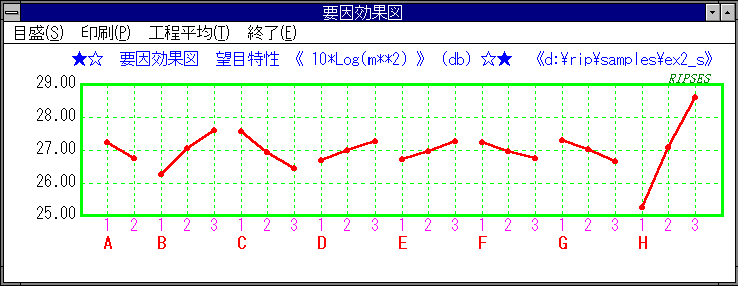
望目特性の場合、はじめは目標値にこだわらないで、SN比を改善します。
SN比に関して最適条件は要因効果図から、A2,B3,C3,D3,E3,F3,G1,H3であることがわかります。
この条件での感度Sと目標値が一致すれば問題はないのですが、差がある場合は、SN比に関係がより少ない要因で、感度Sを調節することになります。
感度Sを推定してみましょう。
ここでは、分散分析表(感度)から、効果の大きい3個の要因、B,C,Hを選び計算を行います。
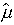 =
=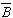 3
+
3
+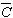 3
+
3
+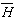 3
−2
3
−2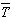 =27.6121+26.4452+28.6007−2×26.9819=28.6941(db)
=27.6121+26.4452+28.6007−2×26.9819=28.6941(db)
目標値は、24.5gであるので、目標値に対するデシベル値との差
28.6941−10log(24.5)2=28.6941−27.7833=0.9108(db)
だけ感度を下げる必要があります。
さいわいなことに、この場合SN比にあまり影響がなく感度Sに影響の大きい因子
H.バネによるBTレバーモーメント(g-mm)
があるので、この因子により、テンションを目標値に調節します。
最適条件
A2,B3,C3,D3,E3,F3,G1,H3〜2
※ Hは確認実験(計算)をして決定します。(調整因子)
最適条件のSN比の推定は、分散分析表(SN比)から、効果の大きい4個の要因を選び計算を行なった場合、
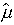 =
=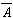 2
+
2
+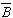 3
+
3
+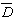 3
+
3
+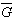 1
−3
1
−3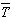
=17.4072+18.8123+17.5255+17.9860−3×16.7922
=21.3545(db)
になります。
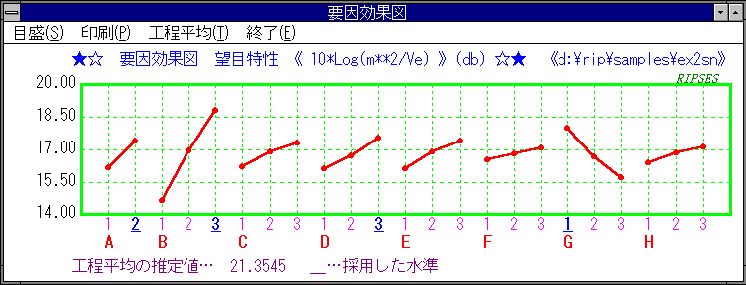
|
推定値は要因効果図の水準値をマウスでクリックすることにより、要因効果図の下に表示されます。 |
|
ここでは最適条件の説明のため、工程平均から推定値を計算をしましたが、実際の作業では、要因効果図の推定に採用する因子の水準値をマウスでクリックすることにより、要因効果図の下に表示されますので、その値を使用します。
採用を取り消すときは因子名をクリックしてください。 |
 |
 |
 第一回・・・パラメータ設計のための特性値 第一回・・・パラメータ設計のための特性値
|
| 品質技術支援サイト ≪HOME≫ | ||||
| RDE | ||||