直交表とその役割

前回、外側のわりつけと誤差因子の調合についてお話をしました。
今回は、内側のわりつけに、なぜ直交表をお勧めしているのかについてお話をしたいと思います。

	直交表の役割
	何度も言うように、パラメータ設計の場合、通常、内側に制御因子を、外側に誤差因子・信号因子をわりつけます。 そして、まず外側因子にわりつけられた信号因子と誤差因子からＳＮ比を求めます。 ＳＮ比を求めるということは、信号因子の効果を維持しながら、誤差の影響ができるだけ少ない制御因子の組み合わせを探すということです。 すなわち、誤差との交互作用を利用し、異なる条件への再現性のある制御因子の組み合わせを探しているのですが、制御因子どうしのＳＮ比に対する交互作用がないことの保証はできません。 そこで、異なる条件への再現性への検査をするために、直交表を用いることになります。 具体的には、直交表に主効果のみをわりつけ、交互作用を交絡させた実験をおこないます。そして主効果のみで最適条件の推定を行い利得を計算します。 そして確認実験で、「その利得が再現するかどうか」を調べて、最適条件で取り上げた制御因子の主効果が信用できるかどうかを検証する必要があります。 ＳＮ比を求めることは、誤差に影響されない制御因子の組み合わせを選ぶことなので、もちろん制御因子どうしの交互作用も小さくする方向を選ぶことにつながると思いますが、最適条件を決める際に、直交表を用いて、主効果をくつがえすような交互作用がないかどうかを確認することが異なる条件での再現性のために必要だと思います。 直交表を用いることによって、「最適条件の選択」の誤りをチェックすることができ、間違った実験結果を後工程に流すことを防止することができます。 品質工学では、異なる下流条件での再現性の検査として利用する点が、従来の実験計画法と大きく異なる点の一つだと思います。
	主効果と交互作用
	パラメータ設計では、直交表に交互作用（制御因子の組み合わせによる効果）をわりつけたり、最適条件を求める時に交互作用を利用することはお勧めできません。 なぜならば交互作用が大きいということは制御因子の最適水準が、他の制御因子の水準により異なることを意味しているので、異なる下流条件でまた、最適条件が変わる可能性が高いからです。 我々企業の目的は、限られた特殊な条件である研究室の中で、すばらしい性能をあげる製品を設計することではなく、研究室の条件とは異なる生産工程や市場条件でも安定して機能する製品を設計することだということを忘れてはいけません。 そのためには、主効果（他の制御因子の水準が変わったときの平均の効果）の積み重ねで最適条件を求める必要があります。 そしてその主効果の大きさくつがえす大きな交互作用がないことを検査する必要があります。そのために使用されるのが、直交表です。
	直交表について
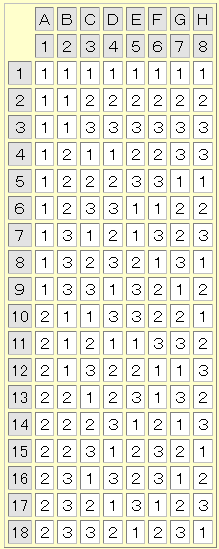
	直交表には、Ｌ４，Ｌ８，Ｌ１２，Ｌ１６などの２水準系直交表とＬ９，Ｌ１８，Ｌ２７，Ｌ３６などの３水準系直交表があります。 このなかで、Ｌ１２，Ｌ１８，Ｌ３６は交互作用が特定列に現れない分散型と呼ばれています。 交互作用分散型は、直交表に主効果のみをわりつけ、交互作用を交絡させた実験をおこない、主効果をくつがえすような交互作用がないかどうかを確認するのに大変適しています。パラメータ設計時、Ｌ１８をお勧めしている理由の一つが交互作用分散型だということです。 直交表の組み合わせは、「１つの列の各水準の中に、他の列の各水準がすべて同回数ずつ現れる」という性質を持っています。このことを直交している」と呼んでいます。 左は、よく使用するＬ１８直交表です。 「１つの列の各水準の中に、他の列の各水準がすべて同回数ずつ現れる」のがわかると思います。 たとえば、１から８列に、ＡからＨという因子を８個わりつけたとします。 ＡとＢを見てみましょう。 Ａ１の水準（実験�ｂP〜�ｂX）にはＢ１が３回、Ｂ２が３回、Ｃ３が３回現れています。 また、Ａ２の水準（実験�ｂP０〜�ｂP８）にはＢ１が３回、Ｂ２が３回、Ｃ３が３回現れています。 ＢとＣはどうでしょうか。 Ｂ１の水準（実験�ｂP〜３，１０〜１２）にはＣ１が２回、Ｃ２が２回、Ｃ３が２回現れています。 また、Ｂ２の水準（実験�ｂS〜６，１３〜１５）にはＣ１が２回、Ｃ２が２回、Ｃ３が２回、同様にＢ３の水準（実験�ｂV〜９，１６〜１８）にはＣ１が２回、Ｃ２が２回、Ｃ３が２回現れています。 「どの列」と「どの列」を見ても直交している事が分かると思います。 他の列の各水準がすべて同回数ずつ現れている（直交している）ので、Ａ１とＡ２の優劣を比較しようとしたとき、他の因子の影響はキャンセルすることができ、（実験�ｂP〜�ｂX）と（実験�ｂP０〜�ｂP８）の平均値を使用することができます。 いいかえれば、他の因子をある条件で固定して比較するのではなく、他の因子の条件をいろいろ変えた条件下で平均値を計算し比較することができます。 すなわち、他の因子の条件をいろいろ変えた条件下で平均値を求めるということは、他の因子が変わっても一貫した効果をもつもののみが、主効果として推定されることになります。主効果は、他の因子の条件が少し位変わっても水準の優劣が逆転しない因子に重点を置いているため、規模という一つの条件が変わっても実験室の結果が生産の場や市場で再現する確立が高くなるということです。 しかし、それはその主効果の大きさくつがえす大きな交互作用がないことを保証しているのではありません。直交表で求めた主効果から計算した利得を、確認実験で検証する必要があります。 主効果が交互作用より十分に大きく信用できるものであれば、その利得は確認実験で再現することになります。

	第一回・・・パラメータ設計のための特性値 第二回・・・因子の分類と一般的な実験の組み方 第三回・・・ＳＮ比とその種類 第四回・・・効率的な設計開発を行うために 第五回・・・ＳＮ比に変換する前に 第六回・・・動特性それとも静特性？ 第七回・・・最適条件を推定してみよう（１） 第八回・・・最適条件を推定してみよう（２） 第九回・・・確認実験は必ず実施しよう 第十回・・・品質評価のためのＳＮ比 第十一回・・・欠測値の処理 第十二回・・・わりつけ（ダミー法と多水準作成法） 第十三回・・・望目特性とゼロ望目特性 第十四回・・・誤差因子の調合 第十五回・・・直交表とその役割 用語集・・・これだけは知っておきたい品質工学用語

品質技術支援サイト ≪HOME≫
RQE	ＲＱＥとは	品質工学のページ	ＲＱＥで解析してみよう	ＲＱＥ開発ルーム
RQC	ＲＱＣの概要	ＲＱＣで解析してみよう	セットアップの手順
RDE	ＲＤＥの概要	ＲＤＥで解析してみよう	セットアップの手順