品質評価のためのＳＮ比

通信工学の世界では、通信機器・回線の良さ・信号の質の良さを表す特性値の一つとして信号と雑音の比の値が、ＳＮ比という名前で使われていました。
品質工学でのＳＮ比はこのＳＮ比の概念を発展させ、「機能の安定性を表す測度」として考案されたものです。

パラメータ設計では、設計を変えることで、機能をばらつかせる環境や劣化などのばらつきの影響を、いかに減衰させるかということが重要で、そのための安定性の評価測度としてＳＮ比を使用します。

具体的には、内側に制御因子を、外側に誤差因子・信号因子を割り付け、最適な制御因子の水準を選択するためにＳＮ比を利用します。詳しくは、「因子の分類と一般的な実験の組み方」を参照してください。

ＳＮ比は安定性の評価測度ですので、パラメータ設計で最適な制御因子の水準を選択するのに使用したのと同様に、計測器や工作機械などの優劣の判断や、測定条件や製造条件選択など、あらゆる機能品質の評価に活用することができます。

今回の講座では、２つのＳＮ比を比較し機能品質の優劣を判断する場合（ＳＮ比を機能品質の評価に用いた例）をご紹介したいと思います。

例題１

簡易型の周波数測定器がＹ社とＨ社から販売されている。
この２台の測定器の性能を比較し購入時の参考としたい。

信号因子としては、基準の発振器にて真値とみなしてよい周波数を作成した。また、複数の波形の対して周波数を計測することが求められているため、誤差因子として波形の種類を変え測定を行った。

以下のデータは、ゼロ点校正後の計測器の周波数測定データである。 ＳＮ比を求め、周波数測定性能の比較をせよ。

Ｙ社の測定器
信号因子 誤差因子	Ｍ１ (１ＭHz)	Ｍ２ (５ＭHz)	Ｍ３ (９ＭHz)	Ｍ４ (15ＭHz)
Ｎ１(正弦波)	1.002	5.011	9.008	14.942
Ｎ２(短形波)	1.008	5.014	9.021	15.088
Ｎ３(三角波)	0.995	5.003	9.012	15.069

Ｈ社の測定器
信号因子 誤差因子	Ｍ１ (１ＭHz)	Ｍ２ (５ＭHz)	Ｍ３ (９ＭHz)	Ｍ４ (15ＭHz)
Ｎ１(正弦波)	1.033	5.175	9.305	15.501
Ｎ２(短形波)	1.038	5.183	9.312	15.508
Ｎ３(三角波)	1.027	5.166	9.283	15.482

信号は、、基準の発振器の周波数
Ｍ１＝１ＭHz
Ｍ２＝５ＭHz
Ｍ３＝９ＭHz
Ｍ４＝15ＭHz

周波数測定器として、複数の波形の対して周波数を計測することが求められているため、誤差因子として波形の種類を変え測定を行った。
Ｎ１＝正弦波
Ｎ２＝短形波
Ｎ２＝三角波

• 上記データがご必要の場合は、以下の４つのファイルを適当なフォルダに保存して下さい。
  clk.021 clk.022 clk.023 clk.02C
  ＲＱＥでファイル(ファイル名…clk)を呼び出します。

この例題では、２台の周波数測定器の性能を比較したいので、周波数測定器が制御因子となり、第１水準がＹ社の測定器、第２水準がＨ社の測定器となります。（１元配置の水準２）
コンボボックスで完備型を選択し、１元配置の水準２と指定してもよいのですが、ＲＱＥにはＳＮ比の比較のためのＬ２というモード（前回の講座「確認実験は必ず実施しよう」で使用したモード）があるのでそちらを利用するとよいと思います。

ゼロ点校正後のデータなのでゼロ点比例式を使用し、周波数計測器の比較をしてみましょう。

もうお分かりだと思いますが、このような計測器の性能を比較する場合でも、望目特性と同様に、はじめは目標値にこだわらないことが大切です。比例定数βは誤差因子間で変化するのでなければ、後で校正することでより正しい測定結果が得られます。使用環境などの誤差因子の条件下で、入出力の比例関係が成立することが重要です。

解析の手順を以下にまとめておきます。

1. 直交表の選択【コンボボックス】
   Ｌ２を選択します。

2. データの新規作成【ファイル(F)】→【新規作成(N)】
   メニューバーから【ファイル(F)】→【新規作成(N)】を選択します。
   

3. ファイル名の入力
   ファイル名を入力します。(ここでは「clk」というファイル名にしました。）

4. 各実験ナンバーのデータ数の入力、直交表のわりつけ
   ひとつの実験ナンバーのデータ数を入力します。
   この場合、信号因子が４水準、誤差因子が３水準なので、各実験ナンバーのデータ数は１２になります。 ＯＫボタンをマウスでクリックし、わりつけを終了します。

5. データの入力【ワークシート】
   ワークシートにデータを入力します。
   データの入力順序は誤差因子の水準より信号因子の水準を、単純な反復より誤差因子の水準を優先して入力して下さい。
   信号因子が４水準、誤差因子を３水準の場合の入力順序は

   Ｍ１Ｎ１，Ｍ１Ｎ２，Ｍ１Ｎ３，Ｍ２Ｎ１，Ｍ２Ｎ２，Ｍ２Ｎ３，Ｍ３Ｎ１，Ｍ３Ｎ２，Ｍ３Ｎ３，Ｍ４Ｎ１，Ｍ４Ｎ２，Ｍ４Ｎ３
   となります。

   データの入力が終了したら、データを保存します。

6. ＳＮ比変換【ＳＮ比(S)】→【ファイル変換(C)】
   メニューバーから【ＳＮ比(S)】→【ファイル変換(C)】を選択します。
   
   • 変換先ファイル名を入力します。(ここでは「clk-sn」というファイル名にしました。）
   • 変換を行うＳＮ比をメニューバーから選択します。
     ここではゼロ点比例式（ＳＮ比）を選択します。
   • メニューバーから【次へ(N)】→【ＳＮ比変換(C)】を選択します
   • スクロールバーで、信号因子の水準４と誤差因子の水準３を設定します。
   • メニューバーから【次へ(N)】→【信号の水準値の入力(S)】を選択します。
   • 信号の水準値を入力します。(1,5,9,15)
   • メニューバーから【次へ(N)】→【ＳＮ比変換(C)】を選択します。
   • Ｓβを推定するときの残差Ｍｒｅｓは誤差に含めてください。
   • ファイル変換を行いました。…」というメッセージを表示し、メニュー画面へ戻ります。

   

ＳＮ比の差を計算してみましょう。
39.745-29.317=10.428(db)

この結果から10.428(db)Ｈ社の周波数測定器が優れていることがわかります。
10.428(db)いわれても…という人は、真数（デシベルにする前）に直してみてください。

10.428(db)は、真数では、11.036に相当するので、Ｙ社の周波数測定器はＨ社の周波数測定器より、校正後の誤差分散が、11.036倍大きいことになります。 すなわち、誤差の範囲では√11.036=3.322倍程、測定精度に差があることになります。

比例式校正の情報が必要な場合は、解析からチェックリストの出力を参照してみてください。

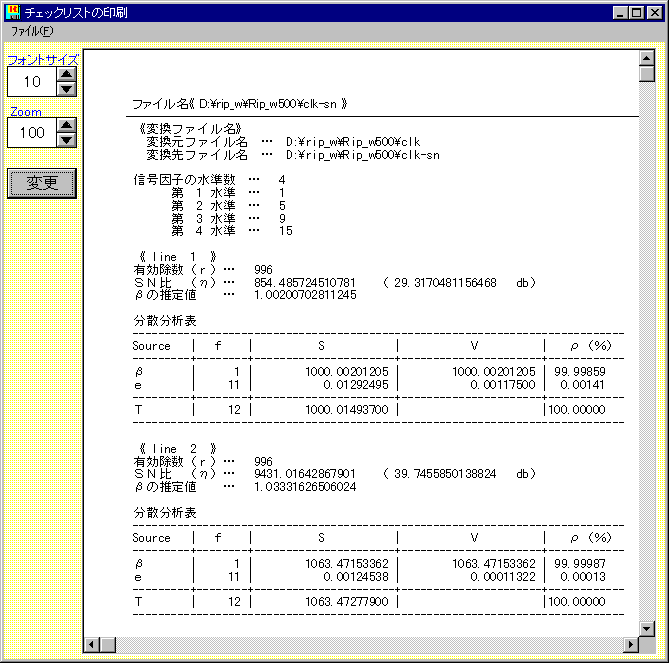
チェックリストでは、ゼロ点比例式の詳しい分散分析表の他、βの推定値、デシベルにする前のＳＮ比η(校正後の誤差分散の逆数)が表示されているので、測定器の校正に活用することができます。

（１次式の場合はαの推定値やｍの推定値も表示されます。)

校正後の誤差分散は　１／η？

感度（β）が違う計測器の誤差を比較する場合、単純に出力（ｙ）の誤差分散を比較することで、計測器や計測方法の優劣を比較することはできません。 出力（ｙ）の誤差分散は、計測器の感度の影響を受けるからです。 私たちが知りたいのは、出力（ｙ）の誤差分散ではなく、計測対象の真値（Ｍ）の誤差分散です。 出力（ｙ）と真値（Ｍ）の関係が以下のような場合 （ｅは、Ｍとｙをゼロを通る直線関係とみなしたときのｙの誤差） ｙ＝βＭ＋ｅ 求めたい真値Ｍは Ｍ＝（ｙ／β）−（ｅ／β） となり、Ｍの推定誤差は（ｅ／β）となることが分かると思います。 すなわち、出力（ｙ）の誤差分散を　σ2　とすると、校正後の誤差分散は σ2／β2　となり デシベルにする前のＳＮ比ηの逆数（１／η）が校正後の誤差分散となります。 ３σ　を考える場合は、±３／√η　となります。 η　はチェックリストに表示されていますのでそれを利用するとよいと思います。

	第一回・・・パラメータ設計のための特性値 第二回・・・因子の分類と一般的な実験の組み方 第三回・・・ＳＮ比とその種類 第四回・・・効率的な設計開発を行うために 第五回・・・ＳＮ比に変換する前に 第六回・・・動特性それとも静特性？ 第七回・・・最適条件を推定してみよう（１） 第八回・・・最適条件を推定してみよう（２） 第九回・・・確認実験は必ず実施しよう 第十回・・・品質評価のためのＳＮ比 第十一回・・・欠測値の処理 第十二回・・・わりつけ（ダミー法と多水準作成法） 第十三回・・・望目特性とゼロ望目特性 第十四回・・・誤差因子の調合 第十五回・・・直交表とその役割 用語集・・・これだけは知っておきたい品質工学用語

品質技術支援サイト ≪HOME≫
RQE	ＲＱＥとは	品質工学のページ	ＲＱＥで解析してみよう	ＲＱＥ開発ルーム
RQC	ＲＱＣの概要	ＲＱＣで解析してみよう	セットアップの手順
RDE	ＲＤＥの概要	ＲＤＥで解析してみよう	セットアップの手順