
 |
最適条件を推定してみよう(1) |
今回は、SN比を求めて要因効果図を作成した後の、最適条件の推定について、ご説明したいと思います。 最適条件を求める場合、大きく分けて二つの場合が考えられます。 一つは、望小特性や望大特性のように平均値とばらつきを総合したSN比から最適条件を求める場合です。 もう一つは、平均値とばらつきを別々に解析し、最適条件を求める(ロバストネスの改善を行った後、チューニング作業を行う二段階設計法)場合です。
わかりやすいように、まず、平均値とばらつきを総合したSN比から最適条件を推定する場合を、望小特性の例題を用いてご説明したいと思います。 そのあとに、平均値とばらつきを別々に解析し、最適条件を求める場合の最適条件の推定方法についてお話したいと思います。
 |
例題1・・・望小特性 |
複写機の地汚れを改善するため、次のような制御因子を取り上げ実験を行なった。 すべて第2水準が現状である。
| A.芯金径 | ・・・ | 2水準 |
| B.表面抵抗 | ・・・ | 3水準 |
| C.トナー | ・・・ | 3水準 |
| D.接触圧 | ・・・ | 3水準 |
| E.シール形状 | ・・・ | 3水準 |
| F.バイアス | ・・・ | 3水準 |
地汚れは0点を理想条件(地汚れ無し)として10段階(0〜9)で評価した。誤差因子として温湿度を3水準設定している。
《わりつけとデータ》
| A | B | C | D | E | F | e | e | 13℃ 20% |
23℃ 50% |
27℃ 80% |
|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||||
| 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 4 | 1 | 4 |
| 2 | 1 | 1 | 2 | 2 | 2 | 2 | 2 | 2 | 3 | 1 | 0 |
| 3 | 1 | 1 | 3 | 3 | 3 | 3 | 3 | 3 | 6 | 5 | 2 |
| 4 | 1 | 2 | 1 | 1 | 2 | 2 | 3 | 3 | 2 | 0 | 1 |
| 5 | 1 | 2 | 2 | 2 | 3 | 3 | 1 | 1 | 2 | 1 | 0 |
| 6 | 1 | 2 | 3 | 3 | 1 | 1 | 2 | 2 | 5 | 0 | 0 |
| 7 | 1 | 3 | 1 | 2 | 1 | 3 | 2 | 3 | 4 | 0 | 0 |
| 8 | 1 | 3 | 2 | 3 | 2 | 1 | 3 | 1 | 4 | 2 | 1 |
| 9 | 1 | 3 | 3 | 1 | 3 | 2 | 1 | 2 | 2 | 0 | 3 |
| 10 | 2 | 1 | 1 | 3 | 3 | 2 | 2 | 1 | 6 | 5 | 2 |
| 11 | 2 | 1 | 2 | 1 | 1 | 3 | 3 | 2 | 7 | 2 | 1 | 12 | 2 | 1 | 3 | 2 | 2 | 1 | 1 | 3 | 7 | 3 | 5 |
| 13 | 2 | 2 | 1 | 2 | 3 | 1 | 3 | 2 | 8 | 1 | 4 |
| 14 | 2 | 2 | 2 | 3 | 1 | 2 | 1 | 3 | 5 | 2 | 1 |
| 15 | 2 | 2 | 3 | 1 | 2 | 3 | 2 | 1 | 6 | 2 | 4 |
| 16 | 2 | 3 | 1 | 3 | 2 | 3 | 1 | 2 | 8 | 4 | 1 |
| 17 | 2 | 3 | 2 | 1 | 3 | 1 | 2 | 3 | 5 | 2 | 2 |
| 18 | 2 | 3 | 3 | 2 | 1 | 2 | 3 | 1 | 6 | 1 | 3 |
「RQE」では、分散分析、工程平均、要因効果図を出力する事ができますので、これらの情報から、最適条件を決定します。
この例題で、「RQE」の出力から最適条件を求めてみましょう。
「RQE」の出力
分散分析表(誤差列をプーリング)
| Source | f | S | V | F0 | S' | ρ(%) |
| 芯金 | 1 | 134.4989 | 134.4989 | 57.99 | 132.1796 | 49.99 |
| 表面抵抗 | 2 | 29.2163 | 14.6081 | 6.30 | 24.5775 | 9.30 |
| トナー | 2 | 31.6180 | 15.8090 | 6.82 | 26.9792 | 10.20 |
| 接触圧 | 2 | 20.8760 | 10.4380 | 4.50 | 16.2372 | 6.14 |
| バイアス | 2 | 29.6273 | 14.8136 | 6.39 | 24.9885 | 9.45 |
| e | 8 | 18.5550 | 2.3194 | − | 39.4294 | 14.91 |
| T | 17 | 264.3915 | 264.3915 | 100.00 |
工程平均
| 因子名 | 水準1 | 水準2 | 水準3 |
| 芯金 | -7.1928 | -12.6598 | |
| 表面抵抗 | -11.5551 | -8.4449 | -9.7789 |
| トナー | -10.3146 | -8.1442 | -11.3202 |
| 接触圧 | -9.1130 | -9.2178 | -11.4481 |
| シール | -10.2169 | -9.5570 | -10.0050 |
| バイアス | -11.2034 | -8.1716 | -10.4039 |
| e | -9.6223 | -9.6982 | -10.4584 |
| e | -9.8347 | -10.3309 | -9.6133 |
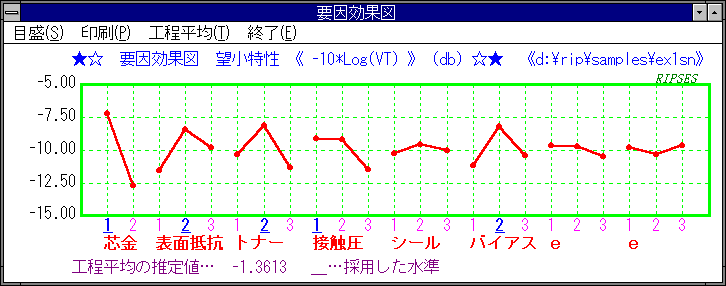
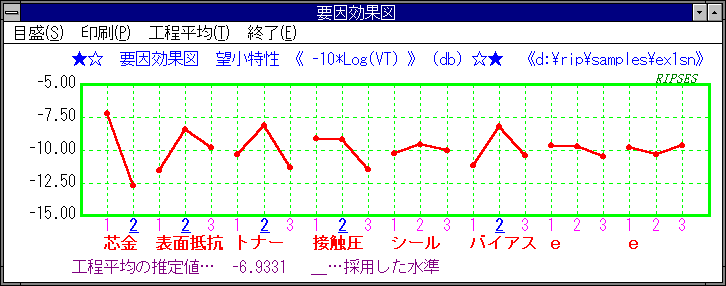
要因効果図
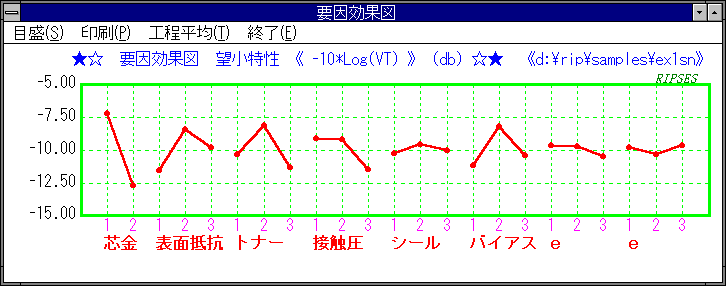
コストに大きな差がない限り最適条件はSN比の最大の組合せ(要因効果図の高い水準の組合せ)です。
この例題での最適条件は、要因効果図から、
A1
B2
C2
D1
E2
F2
であることがわかります。
全部の要因を考えた工程平均は、一般に良過ぎる値になるので、最適条件の推定には誤差を含めて約半分の要因を使って計算します。
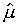
|
=(全体の平均) | +(A1 を採用することによって良くなる部分) |
| +(B2 を採用することによって良くなる部分) | ||
| +(C2 を採用することによって良くなる部分) | ||
| +(D1 を採用することによって良くなる部分) | ||
| +(F2 を採用することによって良くなる部分) |
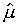 =
=
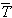 +
(
+
(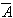 1−
1−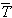 )+
(
)+
(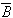 2−
2−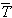 )+
(
)+
(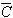 2−
2−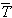 )+
(
)+
(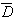 1−
1−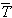 )+
(
)+
(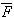 2−
2−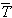 )
)
すなわち
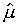 =
=
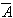 1+
1+
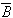 2+
2+
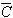 2+
2+
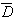 1+
1+
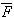 2−
4
2−
4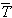
で推定することができます。
推定値は要因効果図を見ながら水準値を選ぶことによって、要因効果図の下に表示されますが
ここでは説明のため、工程平均から計算をして見ましょう。
☆☆ 工程平均 《RP-SN》 ☆☆
| 記号 | 水準1 | 水準2 | 水準3 |
| A | -7.1928 | -12.6598 | − |
| B | -11.5551 | -8.4449 | -9.7789 |
| C | -10.3146 | -8.1442 | -11.3202 |
| D | -9.1130 | -9.2178 | -11.4481 |
| E | -10.2169 | -9.5570 | -10.0050 |
| F | -11.2034 | -8.1716 | -10.4039 |
| e | -9.6223 | -9.6982 | -10.4584 |
| e | -9.8347 | -10.3309 | -9.6133 |
| … 推定に使用 | |
| t | … -9.9263 |
最適条件
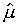 =
=
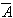 1+
1+
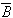 2+
2+
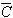 2+
2+
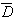 1+
1+
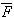 2−
4
2−
4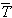
=(-7.1928)+(-8.4449)+(-8.1442)+(-9.1130)+(-8.1716)−4×(-9.9263)=-1.3613
現行条件の工程平均も同様に推定します。
現行条件
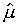 =
=
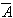 2+
2+
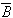 2+
2+
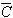 2+
2+
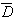 2+
2+
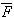 2−
4
2−
4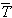
=(-12.6598)+(-8.4449)+(-8.1442)+(-9.2178)+(-8.1716)−4×(-9.9263)=-6.9331
従って、最適条件の利得は
(-1.3613)−(-6.9331)=5.5718(db) になります。
最適条件が決定したら、現行条件と最適条件のもとで、上の利得が再現するかの確認を行います。
約半分の要因で推定を行うのは、全部の要因を考えて利得を求めると良過ぎる推定になるためであり、
実際に最適条件を決定する場合は、コストに関係のない限り、全部の制御因子の良い水準を選定することが大切です。
利得のかわりに、等価平均(ばらつきがないとしたときの点数)で推定することもあります。
望小特性の場合、
−10 log {(y12+ y22+ … + yn2)/n}=η(db)
であるので
最適条件の等価平均yは
y2=100.13613
y=1.17
現行条件の等価平均yは
y2=100.69331
y=2.22
従って、等価平均では、2.22点から1.17点に向上することになります。 等価平均の絶対値は、取り上げた試験条件(さまざまなノイズの組合せ)で異なるので、再現性は利得でチェックして下さい。
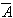 1−
1−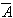 2
=(-7.1928)-(-12.6598)=5.4670 (db)
2
=(-7.1928)-(-12.6598)=5.4670 (db)
|
推定値は要因効果図の水準値をマウスでクリックすることにより、要因効果図の下に表示されます。 |
|
ここでは最適条件の説明のため、工程平均から推定値を計算をしましたが、実際の作業では、要因効果図の推定に採用する因子の水準値をマウスでクリックすることにより、要因効果図の下に表示されますので、その値を使用します。
採用を取り消すときは因子名をクリックしてください。 |
「RQE」マニュアルより引用
 |
 |
 第一回・・・パラメータ設計のための特性値 第一回・・・パラメータ設計のための特性値
|
| 品質技術支援サイト ≪HOME≫ | ||||
| RDE | ||||