
 |
分散分析入門(1) |
完備型実験とは、特性値に影響がありそうな因子(実験に意図的に取り上げた要因を因子と呼びます) について、すべての水準(因子の条件の数)組み合わせの実験を行う方法です。
実験で取り上げた因子の数により、1元配置、2元配置、3元配置・・・と呼んでいます。 基本的には、1因子の水準のみを動かす1元配置と、2因子以上の水準を動かす多元配置(2元配置、3元配置・・・)に分類することができます。
実験を行った後、実験で取り上げた因子が本当に特性値に影響を与えているのか否かを、客観的に調べる方法が分散分析という手法です。
分散分析表の見方を教えて欲しいというご質問を何件かいただきましたので、今回は、最も簡単な1元配置(因子が1つ)の実験を例に、分散分析表についてお話したいと思います。
この例題のRDEでの解析手順は、例題とその解析例の 1元配置(繰り返しがある場合) をご参照ください。
 |
例題1・・・1元配置(繰り返しがある場合) |
ある製造工程では4台の機械で部品を加工している。各機械で5個の部品を加工し寸法を測定したら下記のようなデータを得た。
機械間の違いが部品寸法に影響を与えているか検討せよ。
| 因子A(機械) | 寸法データ(単位 mm) | ||||
| A1 | 487 | 486 | 490 | 487 | 485 |
| A2 | 493 | 490 | 489 | 491 | 492 |
| A3 | 486 | 485 | 485 | 481 | 483 |
| A4 | 485 | 486 | 484 | 486 | 489 |
上記データは、4台の機械で5個づつ部品を加工していますので
4×5=20個
の部品の測定データです。
このデータから機械間の差が部品寸法に影響を与えているかどうか調べるにはどうしたらよいでしょうか。
20個のデータは同一ではなく、ばらつきをもっているので、
とりあえず、それぞれの機械で加工した部品の寸法データの平均値を計算して、平均値を比べてみましょう。
A1の機械で加工した部品寸法の平均値
(487+486+490+487+485)÷5=487
同様に
A2の機械で加工した部品寸法の平均値=491
A3の機械で加工した部品寸法の平均値=484
A4の機械で加工した部品寸法の平均値=486
平均値の変化を見る限り、加工する機械をかえると部品寸法が変化しているように思われます。
しかし、同じ機械A1で加工した部品の寸法データも、485〜490まで、データはばらついています。A2からA4で加工した部品の寸法データも同様です。
このことから、単純に「平均値の変化だけを見て機械の影響があると考える」ことに、疑問を感じるのではないでしょうか。
では、「加工する機械をかえると部品寸法が変化する」「機械をかえると部品寸法に影響がでる」と考えるには、どうしたらよいでしょうか。
二乗の個数(2次形式の係数行列の階数)は自由度と呼ばれ、記号(f)が使用されます。 変動(S)を自由度で割ったものを、分散(V)と呼んでいます。分散は一単位量あたりのばらつきです。
因子の影響によるばらつきには、もちろん誤差分散(偶然によるばらつき)も含まれているので、因子の影響(機械間の違い)がなければ、因子の影響によるばらつき(VA)と誤差分散(Ve)はほぼ同じ値になるのが感覚的にわかると思います。
したがって、その分散の比が1よりはるかに大きければ因子の効果がある、1に近いようであれば因子の効果がないと考えることができます。
因子の影響による分散(VA)と誤差分散(Ve)の比は分散比(F0)と呼ばれています。
この分散比を用いて、通常、危険率(間違えて判断する確立)が5%と1%で定性的な評価が行われます。
危険率1パーセントで有意(間違って判断する確立が1パーセント以下)であれば、*印を2つ、危険率5パーセントで有意(間違って判断する確立が5パーセント以下)であれば、*印を1つ付けるのが慣例です。
因子の影響による変動には自由度分の誤差分散が含まれているので、その誤差分散を除いたものが、純変動(S’)です。純変動を用いて、全変動に対する各因子の影響の割合、寄与率(ρ)を求めることができます。
このように実験データの持っているばらつきを因子の影響大きさのとそれ以外の影響の大きさに分けて、因子の影響の大きさを客観的に判断する方法を分散分析といいます。また、その結果をまとめた表が分散分析表です。
とりあえずRDEを使用して分散分析表を出力してみましょう。
この例題のRDEでの解析手順は、例題とその解析例の 1元配置(繰り返しがある場合) をご参照ください。
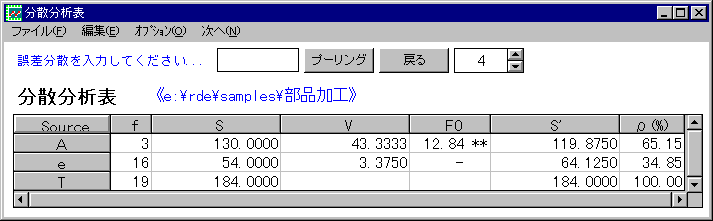
分散分析表をみてみましょう。一番左に因子名として 機械間の影響が「A」、残りの誤差は「e」、合計が「T」として表示されています。
そして左から自由度(f)、変動(S)、分散(V)、分散比(F0)、純変動(S’)、寄与率(ρ)が各因子ごとに表示されています。
分散分析表をみる限り、分散比が12.84と1よりはるかに大きく、危険率1%で有意(*印が2つ)であることから、機械間の差が部品寸法に影響を与えていると考えてもよいのではないでしょうか。
また、機械間の差の寄与率が65%であることから、もし、4台の機械を調整して、それぞれの平均値を同じにすることができれば、全体のばらつき原因のの65パーセントを解決すことができ、おおきな品質改善が期待できます。
収集したデータにいろいろな要因の変動が多く含まれているため、要因単独の効果を同時に比較するのであれば、効率的な実験計画によるデータと分散分析による解析を行ってみるとよいでしょう。
パソコンを使用すれば、データを入力するだけで手軽に分散分析による解析が実施できます。 RDEを活用して統計的品質管理にチャレンジしてみましょう。
品質管理講座
|
|
 第一回・・・分散分析入門(1) 第一回・・・分散分析入門(1)
|
| ≪HOME≫ | ||||
| RDE | ||||